Technical Article - Torque and Horsepower

Oct. 01, 2005 By Gerald Luiz

Email
Print
Discuss

Introduction	The heart of all our vehicles is the engine. We know that it burns fuel to get us moving and over obstacles. We know that torque and power are some kind of metrics to characterize the engine. Much confusion exists over what torque and horsepower are and how they relate. In this article, we try to disspell the confusion. In the next article, we will explain how we put the power to the ground and get things moving via gear reduction.
The Basics	Let's start with some basics. Velocity is speed. It tells how far something moves in a given about of time, e.g. miles per hour. It is a ratio of distance to time: miles/hour or feet/sec. Acceleration is what causes the speed to change. It is a ratio of velocity to time: (feet/sec)/sec. It tells us how much the velocity changes in a given amount of time. Every object has mass. To get an object to move, we must accelerate it somehow to give it velocity. For example, we push on it. Now moving an elephant is much harder than moving a rock. We have to push harder to move the elephant. We quantify this using force. Force = Mass * Acceleration. We see that if we push harder on an object, the acceleration must increase. Something moving at a constant speed has no acceleration, hence needs no force. The metric unit of force is the Newton (N), N=kgm/s/s. In the US, we use the pound (lb or lbs). If we exert a force over a given distance, we have done work. Common units are the Joule (J), Calorie (cal), or pound-feet (lb-ft). We can think of work as energy. Power is how fast we can do work or how fast we can deliver energy, measured by work/time or forcevelocity. Common units are the Watt (W = 1 J/s), lb-ft/s, or horsepower (hp = 550 lb-ft/s). Imagine an elevator with 1000 lbs of load going up 10 stories. If it takes 1 minute or 10 minutes, it takes the same about of energy or work to move the load. Since power is work/time or energy/time, it takes more power to move the load in 1 minute instead of 10 minutes.
Torque	In the automotive world, lots of things move in circles rather than in straight lines. Think of the wheels or engine. Some of the above concepts behave differently and use different names. However, they relate to one another in the same way. Distance is no longer feet or meters, it is revolutions measured in radians. Speed is revolutions (or radians) over time instead of distance over time, for example, revolutions/minute (RPM) or radians/sec. Mass is called inertia. We still need some kind of "push" to get something spinning. Instead of force, we have torque which is "twisting" force so to speak. Like force, torque must be applied to get something to spin faster or slower (accelerate). Torque is measured by the amout of force applied tangentially at a given distance and is given units of force * distance. In the metric system, we would use Newtonmeter (Nm). In the US, we would use poundfeet (lbsft). For some strange reason we usually say "foot pound" instead of "pound feet" but use both lbsft and ftlbs. Think of a wrench. We pull on the handle to turn the bolt. The longer the wrench, the more torque exert on the bolt with the same amount of force.
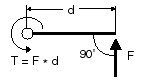Rotational Work and Power	As mentioned above, work is forcedistance. The major source of confusion about torque comes from the units. Torque in lbsft or Nm has the same units as work. Work is energy, torque is a force. Work in the rotational world is still basically forcedistance. Torque is our force and distance is our revolutions in radians (1 revolution = 6.28 radians roughly). We use the same units such as lbft, Nm, or J. The reason the units do not change is that the distance (radians) is a dimensionless quantity. Don't worry about it. Just know that you have to say x lbsft of torque or x lbsft of work or energy to differentiate them. Similarly, power is work/time or forcevelocity. Since work in the rotational world has the same units as in the linear world, power has the same units also. We would use lbsft/s, J/s, W, or hp for example.
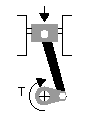
Engines, Torque, and Power	To get our vehicles moving, we use some kind of engine to convert chemical energy (fuel) into useful work. In an internal combustion engine, the fuel in the combustion chamber is ignited by a spark (gasoline) or from compression (diesel), creating high pressure gasses that press down on the pistons. Via the connecting rods, this force pushes the crankshaft throws or arms. Bearings control the crankshaft, allowing it to only rotate. Since each crank arm is offset from the centerline of the crankshaft (the rotational axis), we have torque. Voila. So far we have been kind of simple. The combustion gases develop pressure right away and continue while the crank is turning. Hence, sometimes the force along the connecting rod is not tangential to the crank rotation; it is that way only instantaneously. To further complicate matters, the crank turns at varying rates (engine rpm), different amounts of gasses expanding (throttle), etc. The bottom line is that engines develop differing amounts of torque during operation which is hard to predict. However, we can easily measure it. If we assume that we want maximum torque figures, we assume maximum throttle. All we then worry about is how much torque at what rpm. We end up with a curve. Engine design, fuel systems, etc all change the shape of the torque curve. Note that in most cases, torque rises to some peak value and then decreases. So what about power? If we remember from above, power is torquedistance/time or is torquevelocity. For this discussion, we want to take torque in lbsft and speed in revs/minute and calculate horsepower: Horsepower = torque revs/minute * minute/60 s * 2pi 1/550 Horsepower = torque * revs/minute * 1/5252 In the first line, torque is in lbsft, speed in revs/minute. The third term just converts RPM to revs/s. The fourth term converts revs to radians. The last term is the conversion factor from lbsft/s to horsepower. The second equation just multiplies out the constants to make life easy. 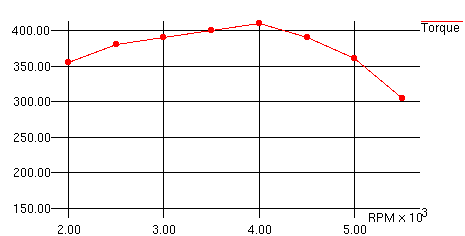Using the above equation, we can add a horsepower curve to our torque graph. Note that the horsepower peak is at a higher rpm than the torque peak. Torque and horsepower are very closely related. We can see that a high revving motor does not need to produce much torque to get lots of horsepower. Similarly, a high torque engine may not develop lots of horsepower.
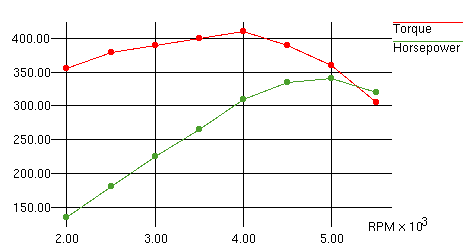Load	One thing that should be considered is that the torque and power graphs illustrate the maximum levels possible. An engine can develop less than that amount at a given rpm. The throttle controls the amount of fuel to the motor and, hence, the torque and power produced. Earlier, we said that force and torque cause acceleration. If we are at a constant speed, how come we continue to need power or torque? The answer is friction or drag. The drag torque tries to slow us down so we add an opposite torque to prevent the deceleration. So in the case of steady speeds, we only need the engine to produce enough torque to compensate for the drag torque. When idling, all the power goes to overcome the drag from friction (assuming no accessories). You can barely touch the throttle to rev the motor 2000 rpm. However, when cruising down the highway at 2,000, you are using much more power to overcome friction, rolling resistance, wind drag, etc. At top speed, 100% of the torque goes to overcome drag.
Continued	In the next article, we will talk about what the torque and horsepower curves mean to us, and how we make them do what we want go get us up and over rocks and down the trail.